Diagram Venn

Assalamu’alaikum warahmatullahi wabarakatuh....

            Pada kesempatan kali ini izinkan saya untuk menjelaskan mengenai diagram venn. Diagram venn ini erat kaitannya dengan himpunan. Untuk memahami secara mendalam apa itu diagram venn, kita harus memahami dulu apa itu himpunan.

Dalam kehidupan sehari-hari, kita sering mendengar atau menggunakan istilah-istilah kelompok, kumpulan, kelasm atau gugus untuk mengungkapkan suatu kumpulan objek atau benda tertentu, misalnya:

·         Kumpulan hewan bertulang belakang (vertebrata)

·         Kumpulan hewan berkaki empat

·         Kelompok tanaman hias

·         Kumpulan mahasiswi di kelas yang memakai hijab

·         Kumpulan mahasiswa di kelas yang tingginya diatas 160 cm

Istilah kelompok, kumpulan, kelas, maupun gugus dalam matematika dikenal dengan istilah himpunan. Konsep tentang himpunan pertama kali dperkenalkan oleh seorang matematikawan asal Jerman bernama Georg Cantor (1845-1918). 

Georg Cantor

Jadi, himpunan adalah kumpulan benda atau objek yang dapat didefinisikan dengan jelas, sehingga dengan tepat dapat diketahui objek yang termasuk himpunan dan yang tidak termasuk dalam himpunan tersebut. Dalam hal ini, yang di maksud dengan sesuatu yang didefinisikan secara jelas adalah yang dapat ditentukan dengan tegas, benda apa yang termasuk dan yang tidak termasuk. Benda-benda yang termasuk dalam sistem himpunan disebut anggota, elemen, atau unsur dari suatu himpunan.

Sekarang, perhatikan kumpulan berikut ini.

·         Kumpulan lukisan indah.

·         Kumpulan wanita cantik di Indonesia.

Kumpulan lukisan indah tidak dapat disebut himpunan, karena lukisan indah menurut seseorang belum tentu indah menurut orang lain. Dengan kata lain, kumpulan lukisan indah tidak dapat didefinisikan dengan jelas. Demikian halnya dengan kumpulan wanita cantik di Indonesia. Wanita cantik menurut seseorang belum tentu cantik menurut orang lain. Jadi, kumpulan wanita cantik bukan termasuk himpunan. Suatu himpunan dapat dinyatakan dengan tiga cara, yaitu:

1.      Dengan kata-kata atau sifat keanggotaan

Menyatakan himpunan dengan kata-kata atau sifat keanggotaan sangat bermanfaat untuk himpunan yang memiliki anggota sangat banyak dan tidak beraturan, karena kita akan mengalami kesulitan saat menuliskan anggota himpunan tersebut satu persatu.

Contoh:

a)      A = { Senin, Selasa, Sabtu}

Penulisan dengan kata-kata atau sifat keanggotaannya adalah :

A = { Nama hari dalam seminggu yang diawali dengan huruf S}

b)      C = {2, 3, 5, 7 }

Penulisan dengan kata-kata atau sifat keanggotaannya adalah:

C = { bilangan prima antara 1-10}

2.      Dengan notasi pembentuk himpunan

Dengan menyatakan suatu himpunan hanya dengan syarat keanggotaan himpunan yang dalam penulisannya dalam bentuk { x | x .... }

Contoh:

a)      Nyatakan himpunan A = {0, 1, 2, 3, 4, 5} dengan notasi pembentuk himpunan!

A = {x | x bilangan cacah kurang dari 6} atau A = {x | x < 6, x bilangan cacah}

b)     Nyatakan himpunan B = {2, 4, 6, 8} dengan notasi pembentuk himpunan!

B = { y | y bilangan asli genap kurang dari 10} atau

B = { y | 1 < y < 10, y bilangan asli genap} atau

B = { y | 2 <  y < 10, y bilangan asli genap.

3.      Dengan mendaftar anggota anggotanya

Dengan cara ini, anggota-anggota himpunan ditulis dalam kurung kurawal dan dipisahkan dengan tanda koma. Pada penulisan dengan cara mendaftar anggota-anggotanya, jika semua anggota dapat ditulis, maka urutan penulisan boleh diabaikan.

Contoh:

a)      P = {nama bulan dalam setahun yang diawali dengan huruf A}

Penulisan dengan mendaftar anggota-anggotanya adalah sebagai berikut

P = { April, Agustus} atau P = {Agustus, April}

b)       W = {x | x < 7, x ∈ A}, dengan A adalah himpunan bilangan asli.

Penulisan dengan mendaftar anggota-anggotanya adalah sebagai berikut

W = {1, 2, 3, 4, 5, 6} atau W = {1, 3, 5, 2, 4, 6}

DIAGRAM VENN

Pada bahasan ini, kita akan mempelajari cara menyatakan suatu himpunan dengan gambar dan diagram disebut diagram venn. Diagram venn pertama kali diperkenalkan oleh John Venn, ahli matematika berkebangsaan Inggris (1834-1923).

John Venn

 Ketentuan dalam membuat diagram venn adalah sebagai berikut:

·         Himpunan semesta digambarkan dengan sebuah persegi panjang dan di pojok kiri diberi simbol S

·         Setiap anggota himpunan semesta ditunjukkan dengan sebuah noktah di dalam persegi panjang itu dan nama anggotanya ditulis berdekatan dengan noktahnya.

Contoh : S = {1, 2, 3, 4, 5}

Diagram Venn dari himpunan S ditunjukkan sebagai berikut:

·         Setiap himpunan yang termuat dalam himpunan semesta ditunjukkan dengan kurva tertutup sederhana.

Misalnya S = {1, 2, 3, 4, 5}

   A = {1, 3, 5}

Karena semua anggota himpunan A termuat di dalam himpunan S, maka himpunan A berada di dalam himpunan S seperti gambar berikut:

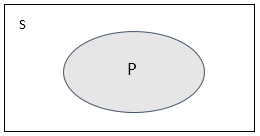
·         Untuk himpunan-himpunan yang mempunyai anggota sangat banyak pada diagram Venn, anggota-anggotanya tidak di gambarkan dengan noktah karena tidak praktis pengerjaannya

Contoh: S = {Mahasiswa Psikologi di Universitas Gunadarma}

              P = { Mahasiswa Psikolodi di kelas 1PA08}   

 

Demikian materi mengenai diagram venn ini saya sampaikan. Saya meminta maaf yang sebesar-besarnya atas segala kesalahan atau kekurangan dalam penyampaian materi ini. Wassalamu’alaikum warahmatullahi wabarakatuh.....

Daftar Pustaka

https://tedjo21.files.wordpress.com/2009/09/07-matematika-kls-7-bab-6.pdf

Nurharini, Dewi dan Tri Wahyuni. (2008). Matematika 1: Konsep dan Aplikasinya: untuk Kelas VI SMP/MTs I. Jakarta : Pusat Perbukuan, Departemen Pendidikan Nasional

Adinawan, M. Cholik dan Sugijono. (2013). Matematika SMP/Mts Jilid 1A Kelas VII Semester 1. Jakarta : Penerbit Erlangga

Picture source:

https://en.wikipedia.org/wiki/Georg_Cantor

https://en.wikipedia.org/wiki/John_Venn